Introduction to probability, discrete and continuous probability distributions
Probability is associated with randomness and uncertainty. It is a mathematical field which is similar to geometry and analytical mechanics. Academicians explained probability as the measure of the likeliness that an event will happen. Probability is enumerated as a number between 0 and 1 (where 0 indicates impossibility and 1 indicates certainty). The higher the probability of an event, there are more chances for the event will occur.
Probability theory characterises a mathematical foundation to concepts such as "probability", "information", "belief", "uncertainty", "confidence", "randomness", "variability", "chance" and "risk". Probability theory is significant for empirical scientists because it gives them a coherent framework to make inferences and test hypotheses based on ambiguous empirical data. Probability theory is also beneficial to engineers building systems that have to operate intelligently in an uncertain world.
There are three major interpretations of probability that include the frequentist, the Bayesian or subjectivist, and the axiomatic or mathematical interpretation.
Probability as a relative frequency: This method interprets the probability of an event as the proportion of times such an e event is expected to occur in the long run. Formally, the probability of an event E would be the limit of the relative frequency of occurrence of that event as the number of observations grows large.
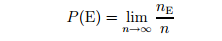
Where nE is the number of times the event is observed out of a total of 'n' independent experiments.
This concept of probability is attractive because it seems objective and links researcher's work to the observation of physical events. One problem with the approach is that in practice researcher can never perform an experiment for an infinite number of times.
Probability as uncertain knowledge: This conception of probability is very beneficial in the area of machine intelligence. In order for machines to operate in natural environments, they need knowledge systems capable of handling the uncertainty of the world. Probability theory provides perfect way to do so.
Probability as a mathematical model: In contemporary period, mathematicians evade the frequentist vs. Bayesian controversy by treating probability as a mathematical object.
Probability measures: Probability measures are usually represented with the letter P (capitalized). Probability measures have to follow three constraints, which are known as Kolmogorov's axioms:
- The probability measure of events has to be larger or equal to zero: P(A) ≥ 0 for all A ∈ F.
- The probability measure of the reference set is 1 P (Ω) = 1
- If the sets A1, A2, . . . ∈ F are disjoint then
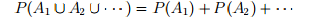
Joint Probabilities: The joint probability of two or more events is the probability of the intersection of those events. For example consider the events A1 = {2, 4, 6}, A2 = {4, 5, 6} in the fair die probability space. Therefore, A1 represents obtaining an even number and A2 obtaining a number larger than 3.
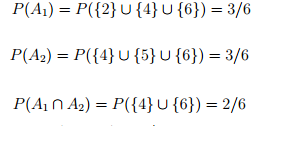
Thus the joint probability of A1 and A2 is 1/3.
Conditional Probabilities: The conditional probability of event A1 given event A2 is defined as follows:
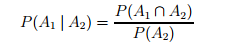
Mathematically this formula amounts to making A2 the new reference set, i.e., the set A2 is now given probability 1 since
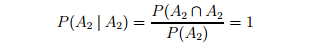
Conditional probability signifies a revision of the original probability measure P. This revision takes into consideration the fact that we know the event A2 has happened with probability 1.
The Chain Rule of Probability: The chain rule, also known as the general product rule in probability theory, allows the calculation of any member of the joint distribution of a set of random variables using only conditional probabilities. The rule is advantageous in the study of Bayesian networks, which defines a probability distribution in terms of conditional probabilities.
Let (A1, A2, . . . , An) be a collection of events. The chain rule of probability tells us a useful way to compute the joint probability of the entire collection
P (A1∩ A2∩ . . . . ∩ An) = P (A1) P(A2│A1) P (A3 │A1∩A2) . . . P(An │ A1∩A2∩ . . . . ∩ An-1)
The Law of Total Probability: the law of total probability is a basic rule associated with marginal probabilities to conditional probabilities. It represents the total probability of an outcome which can be apprehended through several distinct events.
Bayes' Theorem: This theorem, which is credited to Bayes (1744-1809), explains how to revise probability of events in light of new data. This theorem is consistent with probability theory and it is recognised by frequentists and Bayesian probabilists. There is disagreement regarding whether the theorem should be applied to subjective notions of probabilities or whether it should only be applied to frequentist notions.
Bayes' theorem is mathematically represented as the following equation:
P(A/B) |
= |
P(B/A) P(A) |
|
||
P(B) |
Where A and B are events.
P(A) and P(B) are the probabilities of A and B without regard to one other.
P(A | B), a conditional probability, is the probability of A given that B is true.
P(B | A), is the probability of B given that A is true.
Discrete and Continuous Probability Distributions
Probability distributions are categorized as continuous probability distributions or discrete probability distributions. It depends on whether they define probabilities for continuous or discrete variables.A discrete distribution explains the probability of event of each value of a discrete random variable. A discrete random variable is a random variable that has countable values. With a discrete probability distribution, each possible value of the discrete random variable can be associated with a non-zero probability. Therefore, a discrete probability distribution is often presented in tabular form. It is established that if the random variable associated with the probability distribution is discrete, then such a probability distribution is called discrete. Such a distribution is specified by a probability mass function (ƒ). The example given above is an example of such a distribution since the random variable X can have only a finite number of values.
There are five Types of Discrete Distributions:
Binomial Distribution: Probability of exactly x successes in n trials.
Negative Binomial: Probability that it will take exactly n trials to produce exactly x successes.
Geometric Distribution: Probability that it will take exactly n trials to produce exactly one success. (Special case of the negative binomial).
Hypergeometric Distribution: Probability of exactly x successes in a sample of size n drawn without replacement.
Poisson distribution: Probability of exactly x successes in a "unit" or continuous interval.
A continuous distribution defines the probabilities of the possible values of a continuous random variable. A continuous random variable is a random variable with a set of possible values (known as the range) that is infinite and uncountable. A continuous probability distribution varies from a discrete probability distribution in many ways. The probability that a continuous random variable will assume a particular value is zero. Consequently, a continuous probability distribution cannot be expressed in tabular form. As a substitute, an equation or formula is used to define a continuous probability distribution.
The equation used to describe a continuous probability distribution is called a probability density function. All probability density functions satisfy the following conditions:
- The random variable Y is a function of X; that is, y = f(x).
- The value of y is greater than or equal to zero for all values of x.
- The total area under the curve of the function is equal to one.

