Sampling Distributions
Sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are vital in statistics because they offer a major simplification en-route to statistical implication. Mainly, they permit analytical considerations to be based on the sampling distribution of a statistic instead of the joint probability distribution of all the individual sample values. It can be explained that the sample distribution is the distribution that result from the collection of real data. A major attribute of a sample is that it contains a finite (countable) number of scores, the number of scores represented by the letter 'n'. The value of a statistic varies from one sample to another. Therefore, it is a random variable and its probability distribution is known as its sampling distribution.
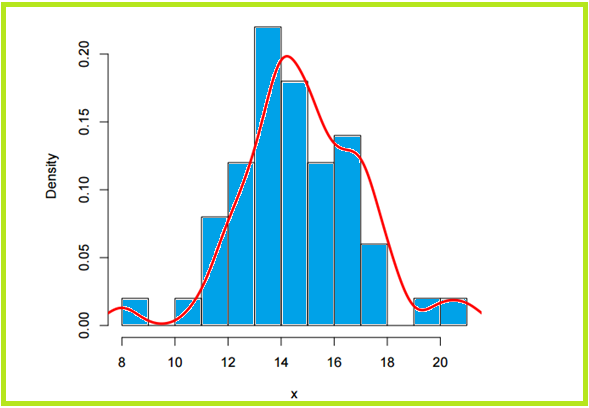
For instance following data develop sampling distribution:
15 14 15 18 15 20 15 16 17 14 17 13 11 14 18 12 17 12 21 8 14 17 14 12 13 15 15 16 17 14 16 13 14 15 18 16 16 17 14 15 16 15 17 12 14 14 13 13 13 14
Sampling distribution
In following example, the rectangle characterizes a large population, and each circle represents a sample of size n. Because the sample entries can differ, the sample means can also differ. The mean of Sample 1 is x1, the mean of Sample 2 is x2, and so on. The sampling distribution of the sample means of size n for this population consists of x1, x2, x3, and so on. If the samples are drawn with replacement, an infinite number of samples can be drawn from the population
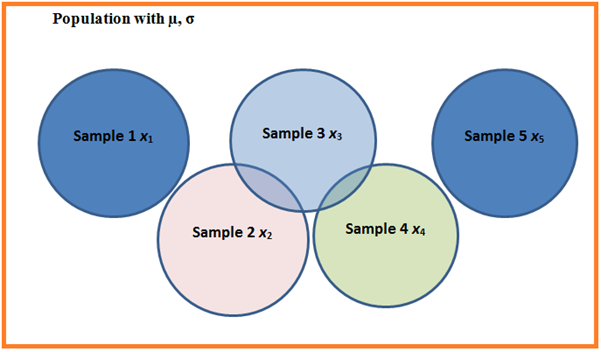
Every statistic has a sampling distribution. For instance, assume that instead of the mean, medians were computed for each sample. The infinite number of medians would be called the sampling distribution of the median.
The sampling distribution of the mean is a distribution of sample means. This distribution may be described with following parameters:
µx and σx
Features of sampling distributions:
There are numerous features of sampling distribution that include:
- The statistic of interest (Proportion, SD, or Mean)
- Random selection of sample
- Size of the random sample (very important)
- The characteristics of the population being sampled
Properties of Sampling Distribution of Mean
- Unbiasedness: Mean of sampling distribution is equal to population mean.
- Efficiency: Sample mean come closure to population mean than any other unbiased estimator.
- Consistency: As sample size increases, variation of sample mean from population mean decreases.
Applications of Sampling Distribution
The sampling distribution like the normal distribution is a descriptive model, so it is used to describe real world situations.It is very useful to make statements about the probability of specific observations occurring.
Investigators/researchers/modelers use it for estimation and hypothesis testing.
To summarize, Sampling is the process of selecting a number of observations (subjects) from all the observations (subjects) from a particular group or population. Sampling distribution is described as the frequency distribution of the statistic for many samples. It is the distribution of means and is also called the sampling distribution of the mean. The sampling distribution is a theoretical distribution of a sample statistic. There is a different sampling distribution for each sample statistic. Each sampling distribution is characterized by parameters, two of which are µ and σ. The latter is called the standard error. The sampling distribution of the mean is a special case of the sampling distribution.

